5.1.2 Bayesian classification

P(C|x) : x에 대한 C 클래스일 확률
P(x|C) : 클래스 C에 속할 때 관측되는 x의 가능도 (likelihood)
P(C) : 클래스 C가 나타날 확률 (prior)


※expX 는 e^X를 의미
확률곱을 더하기의 형태로 만들기 위한 수식. (작은 확률의 곱은 언더플로우를 유발)

만약 100차원 특징벡터 x = (x1,x2,x3...x100)이고, 각 확률이 평균적으로 0.1이라면
0.1^100 = 10^-100이 된다. 그래서 곱연산은 언더플로우를 유발할 수 있음. 그래서 log 형태의 합으로 표현
※log(a*b) = loga + logb

그리고 2개의 클래스가 있다고 가정한다면 이렇게 수식이 나오게 됨.
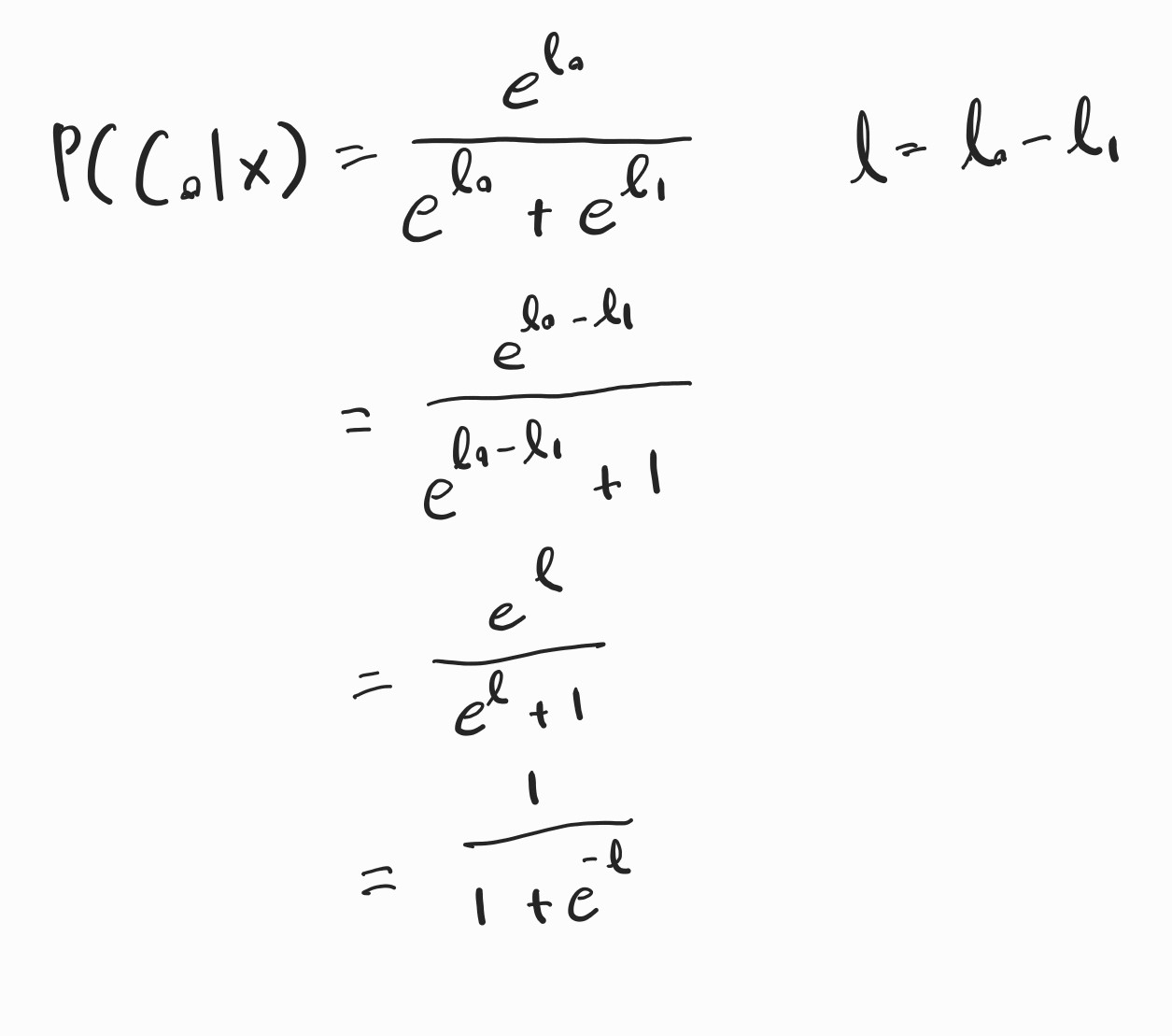
※l = l0 - l1 : log odds or logit / 클래스 0일 확률 대 클래스 1일 확률의 로그 비율

이 수식은 베이즈 분류기에서 클래스별 분포를 다변량 정규분포로 가정했을 때의 수식을 나타냄. (통계학 지식이 없는 저는 간단히 하고 넘어갑니다.)
※위 수식의 시그마 기호는 공분산 행렬을 의미
위 수식은 P(X|C) = 정규화상수 * exp(-1/2거리^2)로 구성
하지만 거리는 유클리디안 거리가 아닌, 마할라노비스 거리를 의미함. 중간에 공분산 행렬의 역행렬 계산이 추가됨.
즉, 분산이 적으면 거리가 커지고, 분산이 크면 거리가 작아짐.


X^T * X = 벡터의 제곱된 길이 = 반지름의 제곱
입력값의 위치와 상관없이 원점에서의 거리만 동일하면 함수값도 동일함.
||X1|| = ||X2|| = r이라면, p(X1) = p(X2)임. 즉, 거리만 같으면 확률 밀도는 같음. (구 대칭 함수, spherically symmetric function)
r = ||X|| ∈ [0,∞)이기 때문에 반지름에 대한 적분의 범위는 [0,∞)임.


어디선가 많이 본 수식의 등장.
σ(z)는 시그모이드 함수임.
벡터 X에 대한 클래스 C0일 확률을 계산함.
가중치 벡터 w는 클래스의 평균 벡터를 마할라노비스 거리 방향으로 정렬함. 공분산을 이용해서 분산이 적은 방향을 찾음. 즉, w는 결정 경계의 방향을 설정함.
바이어스 b는 이 경계를 실제 어디에 위치시킬지를 조정하는 상수임.
5.1.3 Logistic Regression

로지스틱 회귀의 핵심 손실 함수인 binary cross-entropy loss.
t에 1 또는 0을 대입해서 식을 정리하면 이해하기 쉬워짐.
t = 1이면 p가 높을수록 손실이 작아지고, t = 0면 p가 낮을수록 손실이 작아짐. (pi = p(C1|xi))



softmax 기반의 다중 클래스 확률 계산식임.
x에 대해 각 클래스를 softmax를 통해 확률 분포를 계산함.

multi-class cross-entropy loss.
정답 클래스에 해당하는 확률에 로그를 취하고 음수로 바꿔서 손실로 사용함.

각 샘플마다 모델이 정답 클래스에 대해 얼마나 예측했는지 평가함.

크로스 엔트로피 손실함수를 소프트맥스 내부 수식으로 다시 표현함.
손실 = 전체 클래스에 대한 점수의 합 - 정답 클래스의 점수
'Computer Vision > 5. Deep Learning' 카테고리의 다른 글
| [5.5] More complex models (1) | 2025.06.25 |
|---|---|
| [5.4] Convolutional neural networks (0) | 2025.06.13 |
| [5.3] Deep neural networks (깊은 신경망) (0) | 2025.06.08 |
| [5.2] Unsupervised learning (비지도학습) (0) | 2025.06.03 |